| .idea/.idea.FastRng/.idea | ||
| documents | ||
| FastRng | ||
| FastRngTests | ||
| images | ||
| .gitattributes | ||
| .gitignore | ||
| FastRng.sln | ||
| LICENSE | ||
| README.md | ||
FastRng
FastRng is a multithreaded pseudo-random number generator. Besides the generation of uniformly distributed random numbers, there are several other distributions to choose from. For performance reasons, the parameters of the distributions are not user-definable. For some distributions, therefore, different parameter variations are available. If a different combination is desired, a separate class can be created.
Please note, that Math.NET's (https://www.mathdotnet.com/) random number generator is in some situations faster. Unlike Math.NET, MultiThreadedRng is multithreaded. Consumers can use a token to cancel an operation.
FastRng (class MultiThreadedRng) using a shape fitter (a rejection sampler) to enforce arbitrary shapes of probabilities for desired distributions. By using the shape fitter, it is even easier to define discontinuous, arbitrary functions as shapes. Any consumer can define and use own distributions.
The class MultiThreadedRng uses the George Marsaglia's MWC algorithm. The algorithm's implementation based loosely on John D. Cook's (johndcook.com) implementation. Thanks, John, for the inspiration.
Usage
Example code:
using FastRng.Float;
using FastRng.Float.Distributions;
[...]
using var rng = new MultiThreadedRng<float>();
var dist = new ChiSquareK1<float>(rng);
var value1 = dist.NextNumber();
var value2 = dist.NextNumber(rangeStart: -1.0f, rangeEnd: 1.0f);
if(dist.HasDecisionBeenMade(above: 0.8f, below: 0.9f))
{
// Decision has been made
}
Notes:
-
MultiThreadedRngand all distributions are using generic math types: you might usefloat,double, orHalf. -
MultiThreadedRngisIDisposable. It is important to callDispose, when the generator is not needed anymore. Otherwise, the supporting background threads are still running. -
MultiThreadedRngfills some buffers after creation. Thus, create and reuse it as long as needed. Avoid useless re-creation. -
Distributions need some time in creation to calculate probabilities. Thus, create a distribution once and use reuse it. Avoid useless re-creation.
Available Distributions
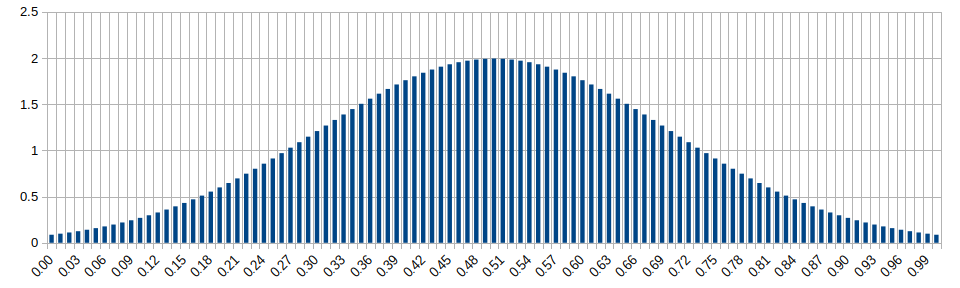
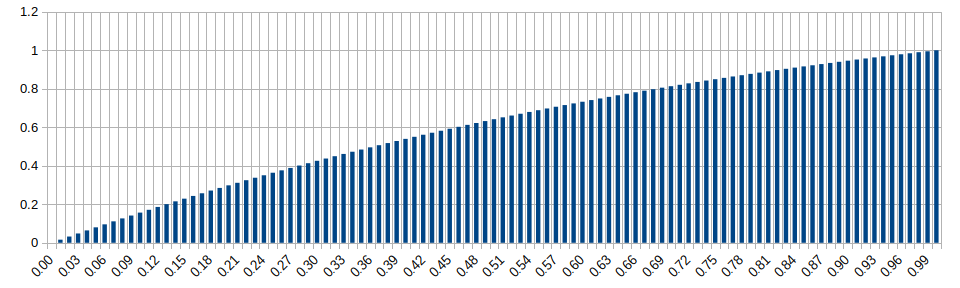
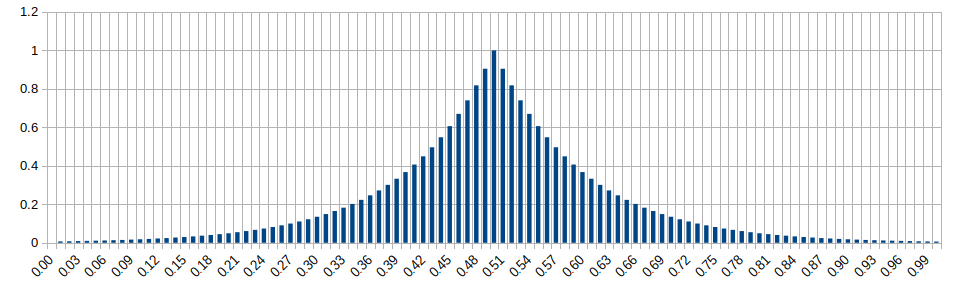
Normal Distribution (std. dev.=0.2, mean=0.5)
Wikipedia: https://en.wikipedia.org/wiki/Normal_distribution
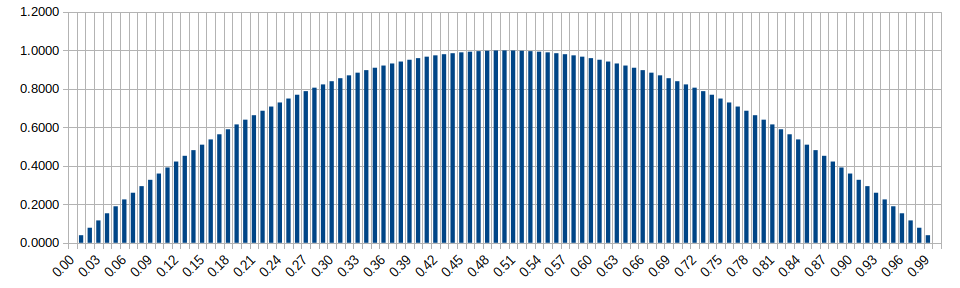
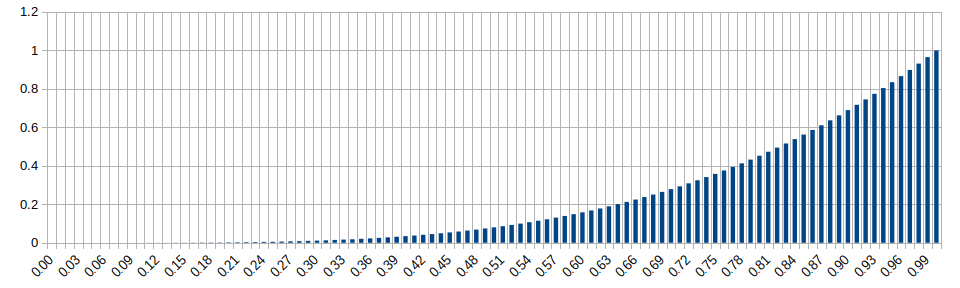
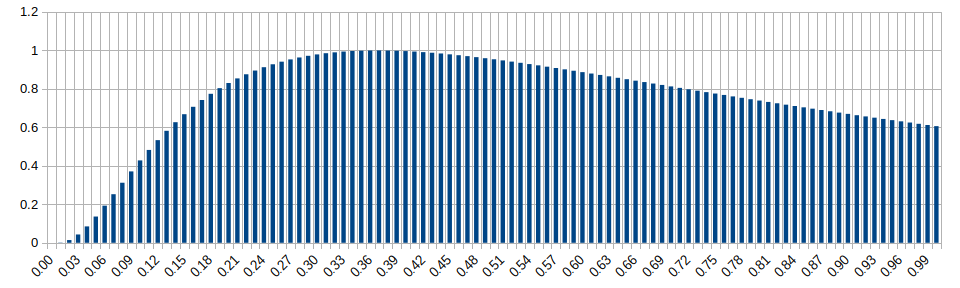
Beta Distribution (alpha=2, beta=2)
Wikipedia: https://en.wikipedia.org/wiki/Beta_distribution
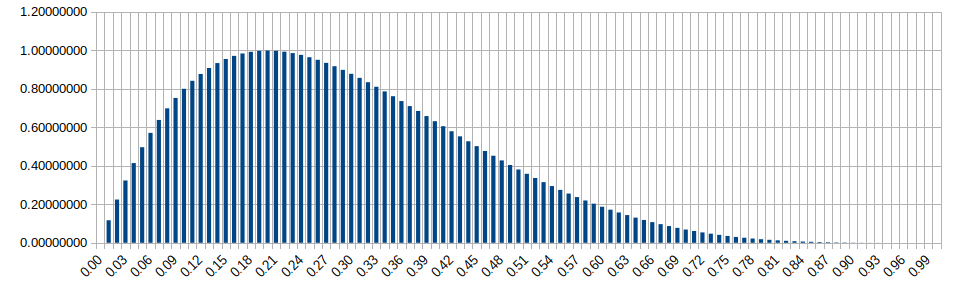
Beta Distribution (alpha=2, beta=5)
Wikipedia: https://en.wikipedia.org/wiki/Beta_distribution
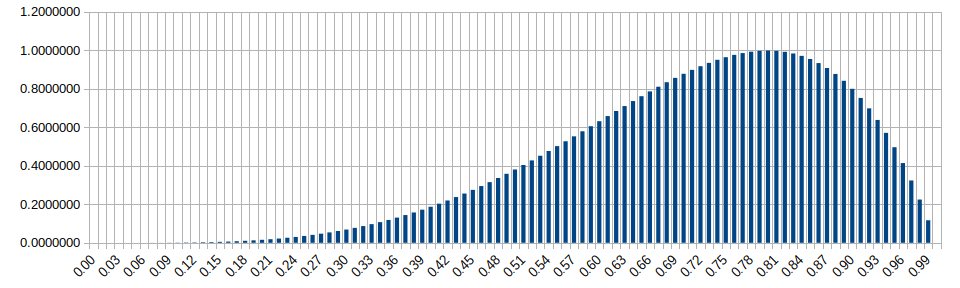
Beta Distribution (alpha=5, beta=2)
Wikipedia: https://en.wikipedia.org/wiki/Beta_distribution
Cauchy / Lorentz Distribution (x0=0)
Wikipedia: https://en.wikipedia.org/wiki/Cauchy_distribution
Cauchy / Lorentz Distribution (x0=1)
Wikipedia: https://en.wikipedia.org/wiki/Cauchy_distribution
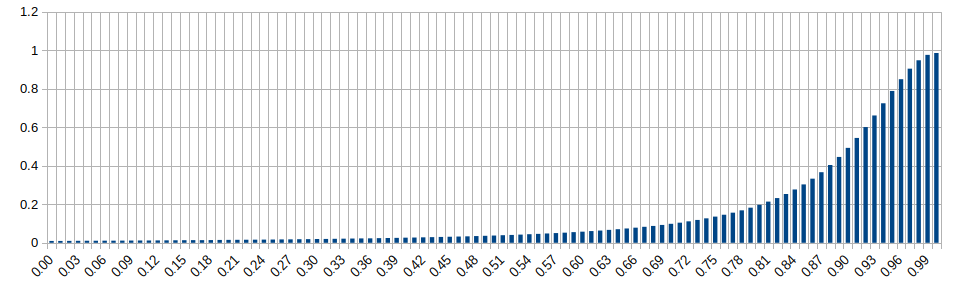
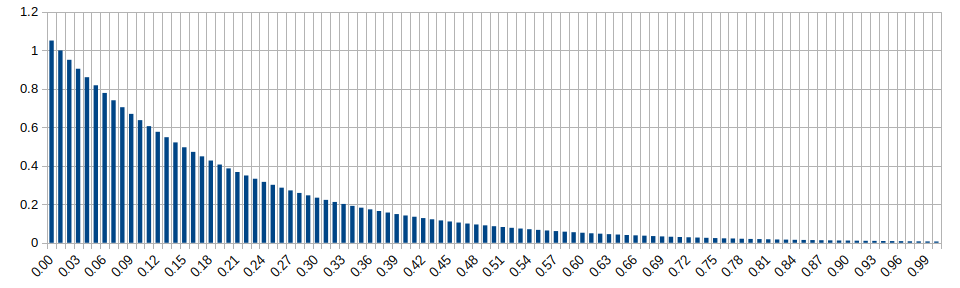
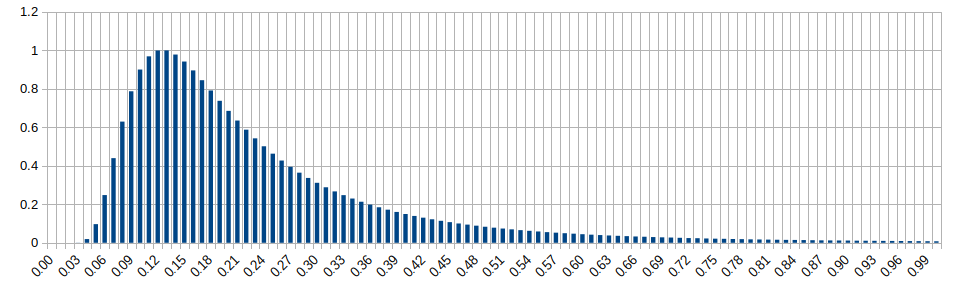
Chi-Square Distribution (k=1)
Wikipedia: https://en.wikipedia.org/wiki/Chi-square_distribution
Chi-Square Distribution (k=4)
Wikipedia: https://en.wikipedia.org/wiki/Chi-square_distribution
Chi-Square Distribution (k=10)
Wikipedia: https://en.wikipedia.org/wiki/Chi-square_distribution
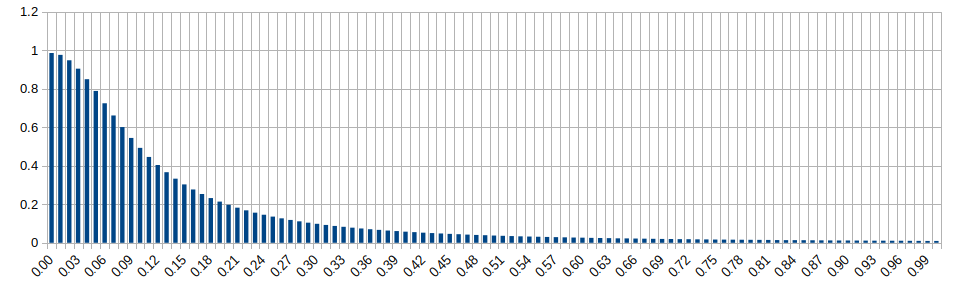
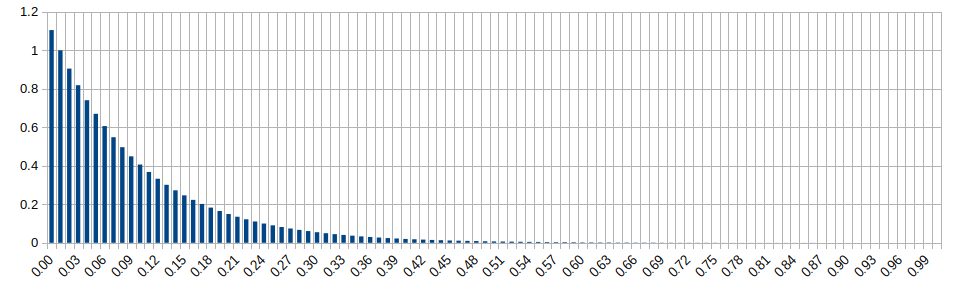
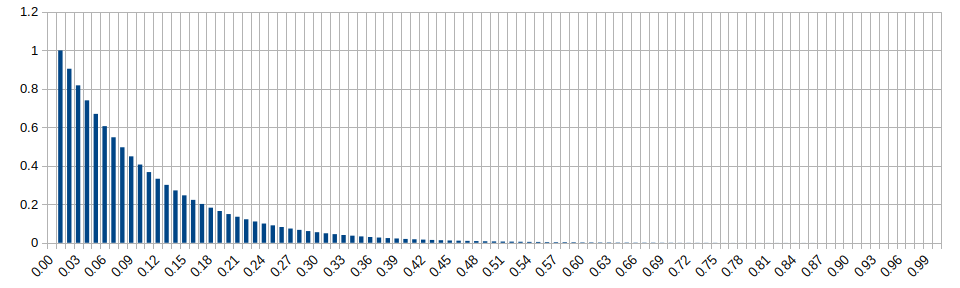
Exponential Distribution (lambda=5)
Wikipedia: https://en.wikipedia.org/wiki/Exponential_distribution
Exponential Distribution (lambda=10)
Wikipedia: https://en.wikipedia.org/wiki/Exponential_distribution
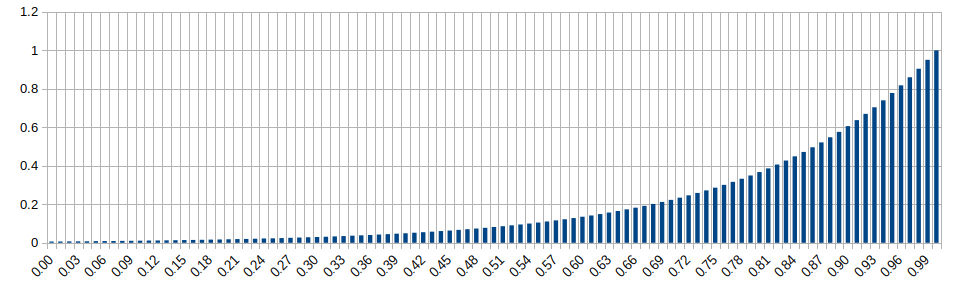
Inverse Exponential Distribution (lambda=5)
Wikipedia: https://en.wikipedia.org/wiki/Inverse_distribution#Inverse_exponential_distribution
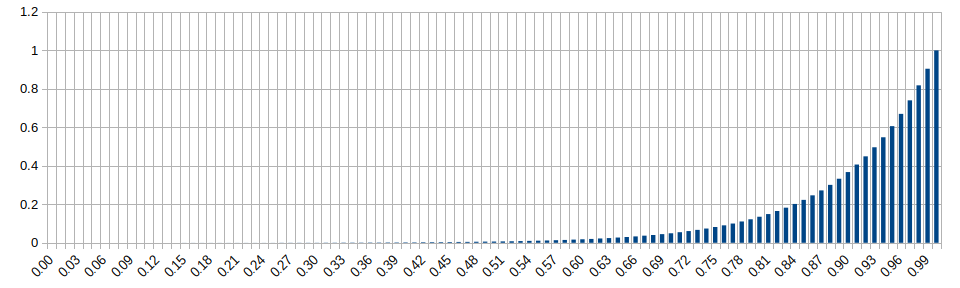
Inverse Exponential Distribution (lambda=10)
Wikipedia: https://en.wikipedia.org/wiki/Inverse_distribution#Inverse_exponential_distribution
Gamma Distribution (alpha=5, beta=15)
Wikipedia: https://en.wikipedia.org/wiki/Gamma_distribution
Inverse Gamma Distribution (alpha=3, beta=0.5)
Wikipedia: https://en.wikipedia.org/wiki/Inverse-gamma_distribution
Laplace Distribution (b=0.1, mu=0)
Wikipedia: https://en.wikipedia.org/wiki/Laplace_distribution
Laplace Distribution (b=0.1, mu=0.5)
Wikipedia: https://en.wikipedia.org/wiki/Laplace_distribution
Log-Normal Distribution (sigma=1, mu=0)
Wikipedia: https://en.wikipedia.org/wiki/Log-normal_distribution
StudentT Distribution (nu=1)
Wikipedia: https://en.wikipedia.org/wiki/Student%27s_t-distribution
Weibull Distribution (k=0.5, lambda=1)
Wikipedia: https://en.wikipedia.org/wiki/Weibull_distribution